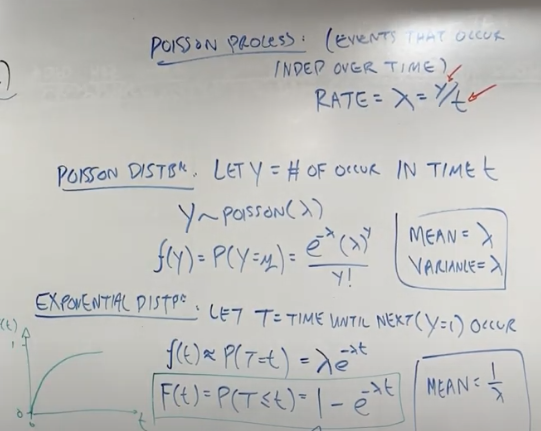Survival Analysis

Survival analysis

Survival analysis is a branch of statistics for analyzing the expected duration of time until one or more events happen, such as death in biological organisms and failure in mechanical systems. - wikipedia

Historically, originally developed and used by acturaries and medical researchers to estimate population lifetimes.

• Video: Censoring

  • Assume: censoring is non-informative - being censored or not is not related to the probablity of event happening

• Video: Survival Function, Hazard, & Hazard Ratio

  • Survival function: S(t) = P(T>t) = prob. of survival beyond time t

  • Hazard: HAZ = P(T< t + dt | T >t) = prob of dying in next few seconds, given alive now

  • Hazard ratio (HR) , prob of dying in next few seconds given exposure vs. not

    \( HR = {HAZ, x=1 \over HAZ, x=0} \)

• Video: comparing 3

  model	Kaplan-Meier	Exponential	Cox-PH model
  type	non-parametric	parametric	semi-parametric
  prob	Simple can est S(t)	can est S(t) and HR	hazard can fluctuate with time can est HR
  con	No functional form cannot est HR *	not always realistic assume constant HAZ Weibull model allows haz to proprotially ↗ or ↘ with time)	cannot est S(t)

• Video: part 4- Kaplan-Meier model

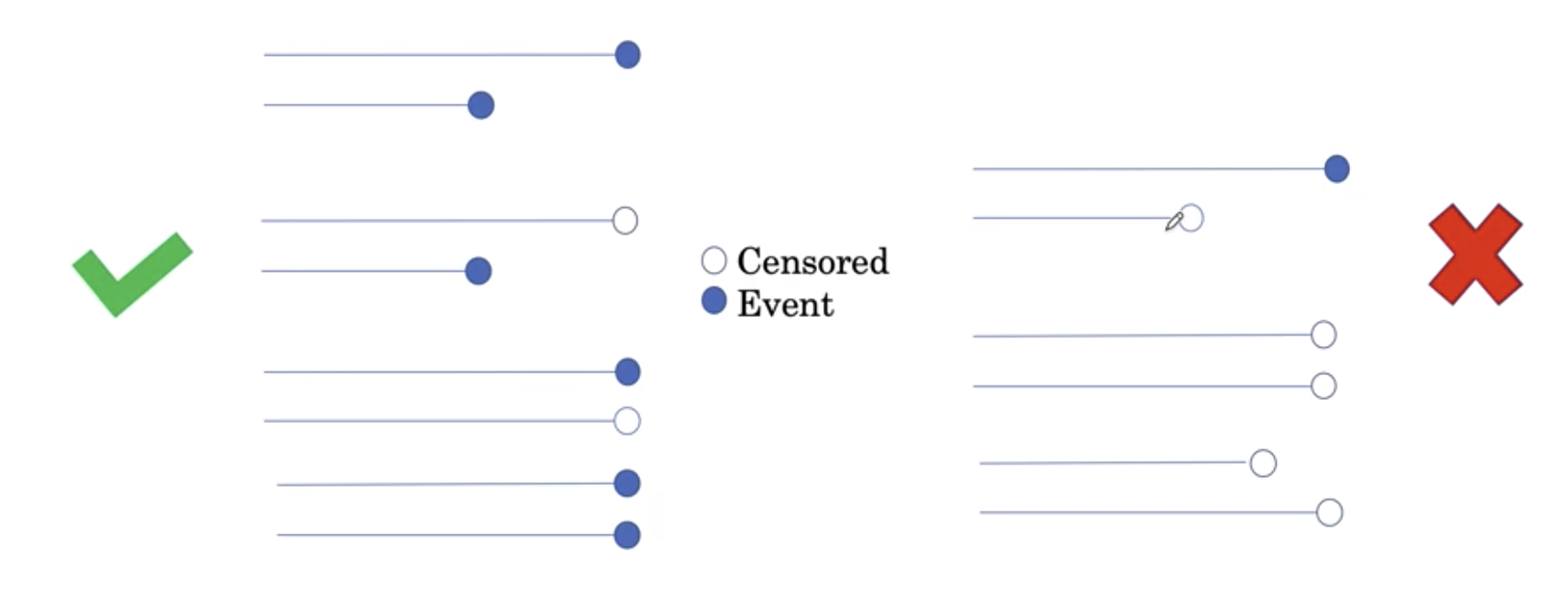
  • Process to compute the survival curve:
  • censored data get incorporated for all the prob. calculations before they drop out
  • a tick indicate censored data
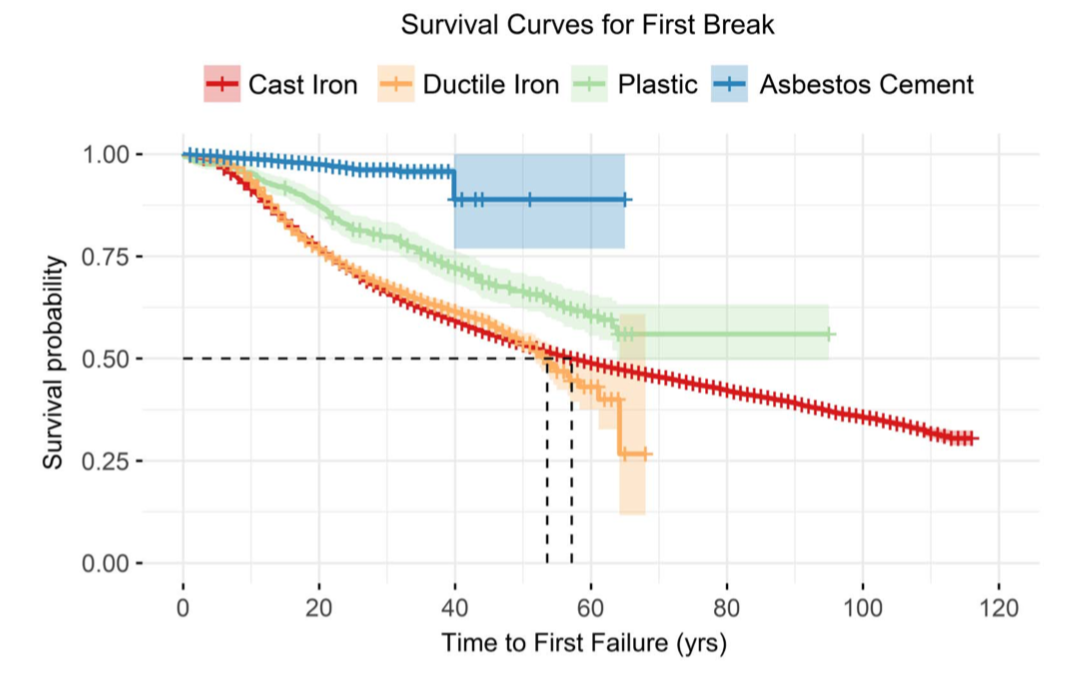
  • example graph from water pipe break paper

• Video: Exponential Model

• Video: Exponential vs Weibull vs Cox Proportional Hazards

  • Overall:
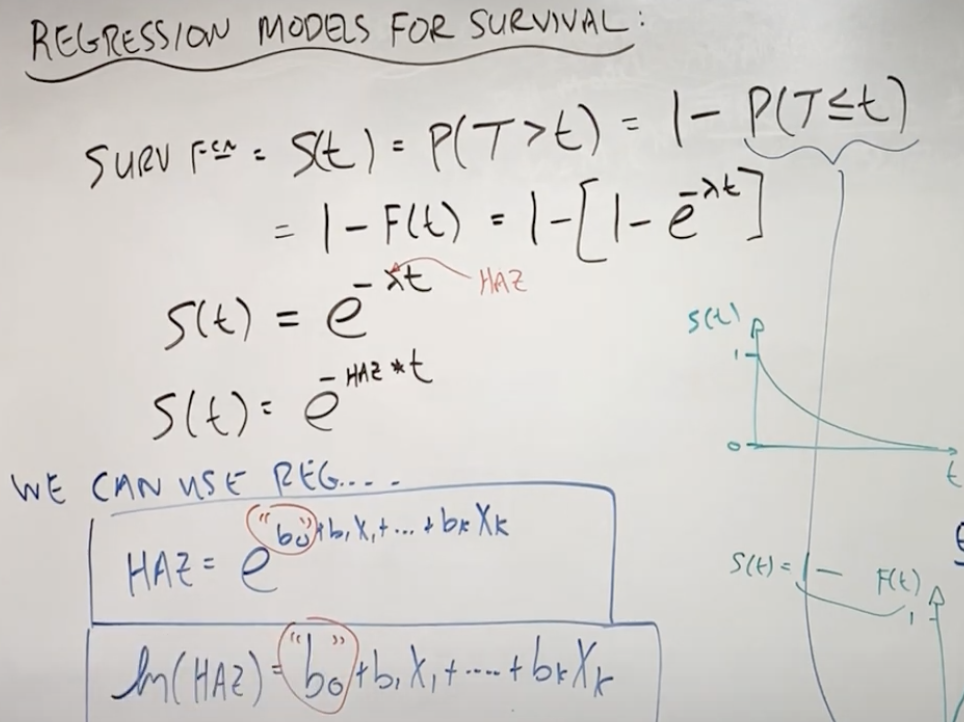
    • \( Survival Function = S(t) = P(T>t) = e^{-HAZ*t} \)
    • \( HAZ = e^{ b{0} + b{1}x{1} + b{2}x{2} + ... + b{k}x_{k}} \)
    • \( \ln(HAZ) = b{0} + b{1}x{1} + b{2}x{2} + ... + b{k}x_{k} \)
    • \( b_0 \) is \( \ln(HAZ) \) for reference (at T=0)
  • Exponential
    • \( b_0 \) is constant -> constant hazard
  • Weibull
    • \( b_0 \) is proprotional to time: \( \ln(\alpha) \ln(t) + b_0 \) => \( b_0 \)
    • \(\alpha = 1 \) - constant hazard
    • \(\alpha > 1 \) - hazard increase with time
    • \(\alpha < 1 \) - hazard decrease with time
  • Cox Proportional Hazards
    • \( b_0 \) is a function of time
    • the algo can estimate \( b_1, b_2, .... \) without having to specify the funtion for \( b_0 \)
    • good for analyzing hazard ratios: how effective is treatment A vs B, exposure or non-exposure
    • can't do predictive models on survival

  Lifelines: Survival analysis in python

• Talk from the author

• Docs: https://lifelines.readthedocs.io/en/latest/index.html

Coursera: AI for Medical Prognosis

• prognosis vs diagnosis:
  • prognosis = predicting the likely or expected development of a disease
• examples in medical practice:
  • CHA2DS2-VASc score for atrial fibrillation
  • MELD score for end-stage liver desease:
    • \( ln \) terms
    • contain an intercept = if all other values is 0, expected risk score
  • ASCVD (Atherosclerotic Cardiovascular Disease) Risk Calculator
    • interaction terms - capture dependence btw variables
      • e.g. blood pressure has less effect of risk when patient is older

Evaluating risk scores

• Concordant Pairs:

  • 
  • Concordant = patient with worse outcome has higher risk score
  • if outcome ties => exclude
  • if outcome different => permissible pair => inlcude
  • rule:
    • +1 for permissible pair that is Concordant
    • +0.5 for permissible pair with risk tie (outcome different, but same risk score)

• C-index

  \( C-index = { Count{concordant} + 0.5 Count{ties} \over Count_{permissible}} \)

• Applying c-index on censored data - Harrel's C-Index

  • patient A & B both not censored => always permissible, even if A & B has same time-to-event
  • patient A & B both censored => not permissible
  • patient A censored, B not censored:

    - if A < B - not permissible
    - if A >= B - permissible